今回は移動速度論における熱、物質、運動量のアナロジーを理解する第一歩として、まずは移動現象にてついて説明します。また、移動現象を表す基本法則であるフーリエの法則、フィックの第一法則、ニュートンの法則についても紹介します。
移動速度式
まず、物質の移動現象は以下の移動速度式で表すことができます。
$$ J=-K\frac{ \partial L }{ \partial r } $$
このとき、
\(J [(物理量)/(m^2\cdot s)]\): 流束、flux(単位時間に単位面積を通過していく物理量)
\(\frac{ \partial L }{ \partial r } [(推進力となる物理量)/m]\): 推進力、driving force(ある物理量の勾配 )
\(K\): 輸送係数、移動係数(移動速度式における比例定数)
を表しています。
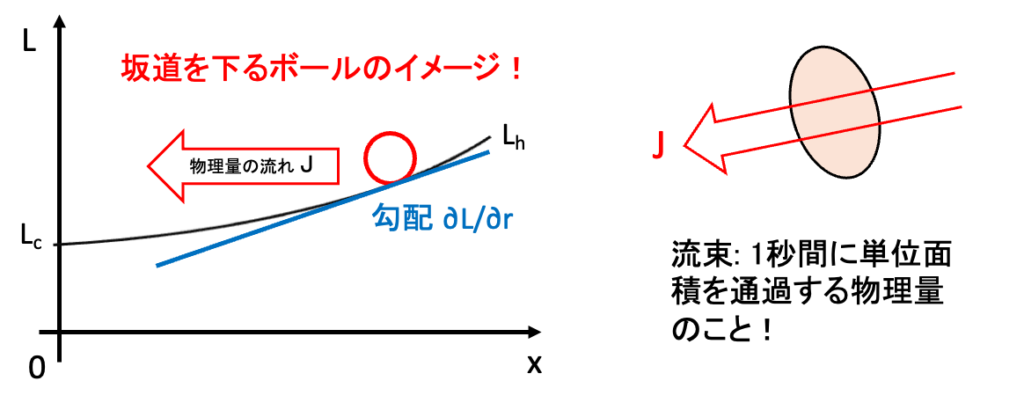
物理量 \(L\)の空間勾配を推進力として、それに比例した大きさの流束\(J\)が生じる現象を移動現象といいます。上の式にマイナスがつくのは、推進力である物理量\(L\)の大きい方から小さい方に向けて流束が移動することを表しています。
ここで 、物質を構成する分子は絶えず乱雑な運動をしており、互いに衝突を繰り返すうちに均一な分布へ近づく性質があります。これを拡散といい、移動現象は拡散の結果として生じるものです。
拡散の特徴は以下の式で表されます。
$$J=-D\frac{ \partial l }{ \partial r }$$
このとき、
\(J [(物理量)/(m^2\cdot s)]\): 流束
\(\frac{ \partial l }{ \partial r } [((物理量)/m^3)/m]=[(単位体積あたりの物理量)/m]\): 推進力
\(D\): 拡散係数
を表しています。
この式は移動速度式を式変形して、推進力の勾配の単位を単位体積あたりの流束の物理量に一致させたものと見ることができます。
熱移動(熱伝導、熱交換)
熱伝導とは、固体または静止している流体の内部において高温側から低温側へ熱が伝わる現象のことです。熱伝導による熱流束は温度勾配に比例し、以下のフーリエの法則によって表されます。
$$q=-\lambda\frac{ \partial T }{ \partial r }$$
このとき、
\(q [(J)/(m^2\cdot s)]=[W/m^2]\): 熱流束
\(T[K]\): 温度
\(\frac{ \partial T }{ \partial r } [(K)/m]\): 温度勾配
\(\lambda (k, \kappa で表すこともある)[J/(m\cdot s\cdot K)]\): 熱伝導率
を表しています。
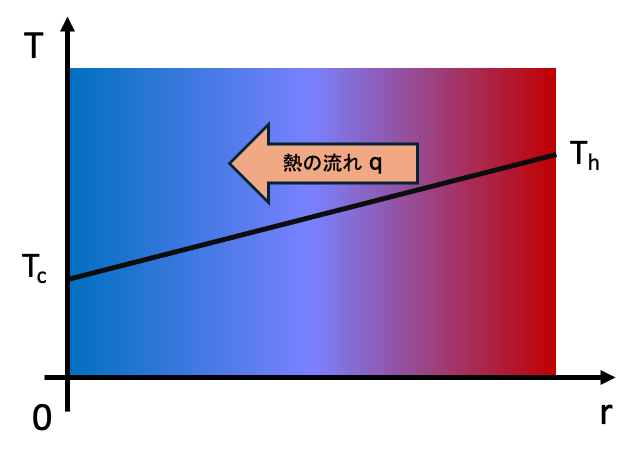
熱伝導率は物質によって異なり、その値が大きいほど熱が伝わりやすくなります。一般に固体>液体>気体の順に高く、金属の中では銀>銅>金>アルミニウムの順に高くなっています。1
物質の密度\(\rho [kg/m^3]\)と比熱\(C_p [J/(kg\cdot K)] \)が一定であるとして、熱量勾配の比例式に変形すると、単位体積あたりの熱量は\(\rho C_p T [J/m^3]\)なので、
$$q=-\frac{\lambda}{\rho C_p}\frac{ \partial (\rho C_p T) }{ \partial r }=-\alpha\frac{\partial (\rho C_p T)}{\partial r} $$
このとき、
\(\alpha [m^2/s] \): 熱拡散率
を表しています。
この式より、熱伝導率と熱拡散率の関係式が得られます。
$$ \alpha = \frac{\lambda}{\rho C_p} $$
物質移動
物質移動による拡散流束は濃度勾配に比例し、以下のフィックの第一法則によって表されます。
$$J=-D\frac{ \partial C }{ \partial x }$$
このとき、
\(J [(kg)/(m^2\cdot s)]\): 質量流束
\(C[kg/m^3]\): 質量濃度
\(\frac{ \partial C }{ \partial x } [(kg/m^3)/m]\): 質量濃度勾配
\(D [m^2/s]\): 拡散係数
を表しています2。
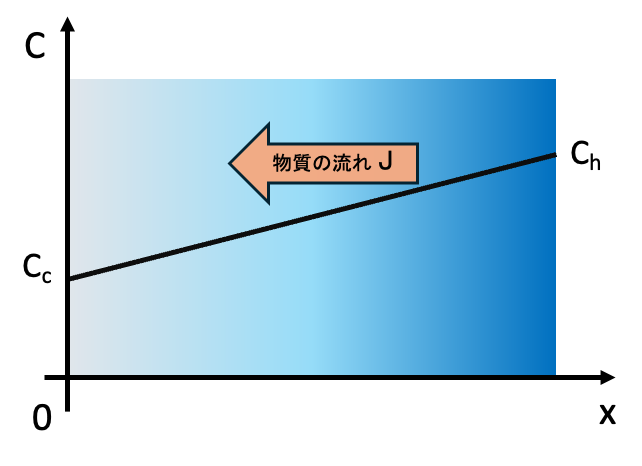
拡散係数が大きいほど物質が速く拡散します。拡散係数については、大きい分子ほど小さくなること、空気中では液体中より約一万倍大きいこと、温度が高いほど大きくなることなどが知られています。
なお、すでに質量流束の物理量と、推進力となる単位体積あたりの物理量が一致しているため、式変形は存在しません。
運動量移動
まず、剪断応力について説明します。
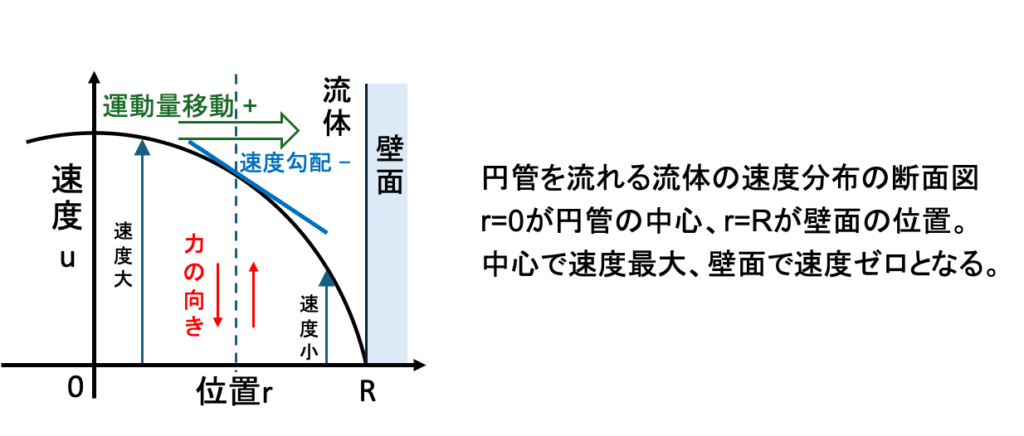
剪断応力とは流体の粘性によって生じる単位面積あたりの流体同士の摩擦力のことです。下図のように、壁面を右に動かすと壁面と接している流体は摩擦によって引っ張られて右に、壁面は反作用により左に力を受けます。
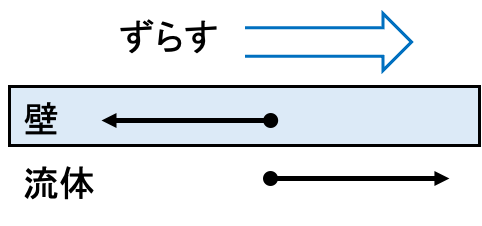
剪断応力は流体分子同士の摩擦力によっても生じます。速度の大きい流体が速度の小さい流体を引っ張ることで、速度の小さい流体が流れの方向に、速度の大きい流体が流れと逆の方向に力を受けます。これを微視的に見たとき、仮想面で分子同士が衝突し、速度の交換・変化が起こることで、下図の左から右に運動量が移動したと見ることができます。
流体の粘性は次のように考えることができます。
① 流体内部に摩擦力を生じて、流れを止めようとする性質。(剪断応力の強さ)
② 流体分子の運動量を減少させて、流動しにくくする性質。(運動量移動の程度)
運動量移動による運動量流束(剪断応力)は速度勾配に比例し、以下のニュートンの法則によって表されます。
$$\tau=-\mu\frac{ \partial v_x }{ \partial y }$$
このとき、
\(\tau [(運動量)/(m^2\cdot s)]=[(kg\cdot m/s)/(m^2\cdot s)]=[(kg\cdot m/s^2)/m^2]=[N/m^2]=[Pa]\): 運動量流束(剪断応力)3
\(v_x [m/s]\): 速度
\(\frac{ \partial v_x }{ \partial y } [1/s]\): 速度勾配
\(\mu [Pa\cdot s]=[kg/(m\cdot s)]\): 粘性係数、粘度
を表しています。
粘性係数が大きいほど粘り気が強く流体は流れにくくなります。液体の粘度は気体の100倍程度であることや、気体の粘度は温度が高くなると大きくなる一方で、液体はその逆であることなどが知られています。
流体の密度\(\rho [kg/m^3]\)が一定であるとして、運動量勾配の比例式に変形すると、単位体積あたりの運動量は\(\rho v_x [(kg\cdot m/s)/m^3]\)なので、
$$\tau=-\frac{\mu}{\rho}\frac{ \partial (\rho v_x) }{ \partial y }=-\nu\frac{\partial (\rho v_x)}{\partial y} $$
このとき、
\(\nu [m^2/s] \): 動粘性係数、動粘度
を表しています。
この式より、粘度と動粘度の関係式が得られます。
$$ \nu = \frac{\mu}{\rho} $$
まとめ
フーリエの法則: $$ q=-\lambda\frac{ \partial T }{ \partial r }=-\alpha\frac{\partial (\rho C_p T)}{\partial r}, \alpha = \frac{\lambda}{\rho C_p}$$ フィックの第一法則: $$ J=-D\frac{ \partial C }{ \partial x }$$ ニュートンの法則: $$\tau=-\mu\frac{ \partial v_x }{ \partial y }=-\nu\frac{\partial (\rho v_x)}{\partial y}, \nu = \frac{\mu}{\rho}$$
今回は移動現象についての基本法則として、フーリエの法則、フィックの第一法則、ニュートンの法則について紹介しました。これらは元々独立して発見されたのですが、背景には原理として分子の運動が共通してあることから、アナロジーによって同じ形になるのが興味深いところですね。
コメント