無次元数まとめ

今回はプラントル数、レイノルズ数、ヌッセルト数などの無次元数についてまとめて紹介します。

無次元数は、化学工学において大切な概念です。ある系や反応において、それがどのような特徴を持つのかを理解するのに役立つだけでなく、無次元であるため反応のスケールに依存せず、実験室から工業用のプラントにスケールアップする際に統一的な指標として利用することができるという意義があります。

拡散係数の比

まず、無次元数のうち、拡散係数の比で表されるものを紹介します。

熱拡散率\(\alpha\)、拡散係数\(D\)、動粘度\(\nu\)は全て単位が\([m^2/s]\)なので、これらの係数の比をとったものはそれぞれの物理量の移動のしやすさの比を表した無次元数となります。

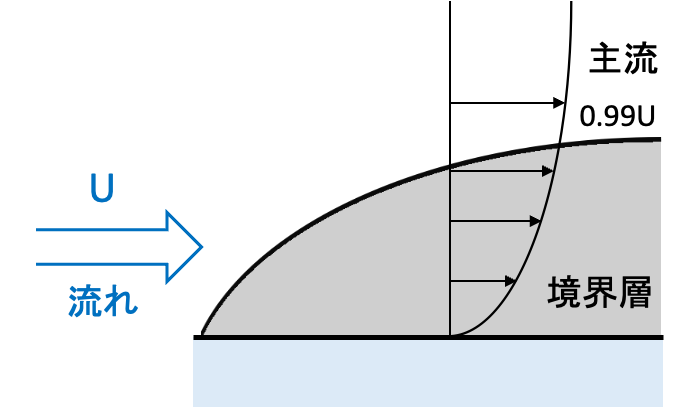
また、各物理量について物質近傍に形成される値の小さい領域を境界層といい、無次元数は境界層の厚さの比も表します。一般に主流の99%に達するまでの領域を境界層といいます。

ルイス数 \(Le\)

ルイス数\(Le\)は熱拡散率\(\alpha\)と拡散係数\(D\)の比で定義されます。

$$Le=\frac{\alpha}{D}=\frac{\lambda/\rho C_p}{D}=\frac{\lambda}{\rho C_p D}$$

\(Le\)が1のとき温度境界層と濃度境界層の厚みが等しく、伝わりやすさが同程度となります。1より大きくなるほど温度境界層の方が厚く、熱エネルギーの拡散の度合いが分子の拡散の度合いよりも大きくなります。1より小さいとその逆となります。

シュミット数 \(Sc\)

シュミット数\(Sc\)は動粘度\(\nu\)と拡散係数\(D\)の比で定義されます。

$$Sc=\frac{\nu}{D}=\frac{\mu/\rho}{D}=\frac{\mu}{\rho D}$$

\(Sc\)が1のとき速度境界層と濃度境界層の厚みが等しく、伝わりやすさが同程度となります。1より大きくなるほど速度境界層の方が厚く、運動エネルギーの拡散の度合いが分子の拡散の度合いよりも大きくなります。1より小さいとその逆となります。

プラントル数 \(Pr\)

プラントル数\(Pr\)は動粘度\(\nu\)と熱拡散率\(\alpha\)の比で定義されます。

$$Pr=\frac{\nu}{\alpha}=\frac{\mu/\rho}{\lambda/\rho C_p}=\frac{\mu C_p}{\lambda}$$

\(Pr\)が1のとき速度境界層と温度境界層の厚みが等しく、伝わりやすさが同程度となります。1より大きくなるほど速度境界層の方が厚く、運動エネルギーの拡散の度合いが熱エネルギーの拡散の度合いよりも大きくなります。1より小さいとその逆となります。

移流と拡散の比

移流（または対流）とは空間内の物質の移動によって、直接的に物理量が移動することです。

物理量流束の移流項と拡散項の比をとったものは、物理量移動においてどちらが支配的かを表す無次元数となります。

ペクレ数 \(Pe\)

流れ場の代表速度を\(u\)、代表長さを\(L\)、代表温度差を\(\Delta T\)とすると、強制対流熱伝達と熱伝導それぞれの熱流束は以下のようになります。

$$(移流項)=(単位体積あたりの熱量) \times (流速)=\rho C_p \Delta T u$$

$$(拡散項)=-\lambda \frac{\partial T}{\partial r}=\lambda \frac{\Delta T}{L}=\frac{\lambda \Delta T}{L}$$

従って、熱流束の移流項と拡散項の比で定義されるペクレ数\(Pe\)は以下のようになります。

$$Pe=\frac{\rho C_p \Delta T u}{\lambda \Delta T / L}=\frac{\rho C_p u L}{\lambda}=\frac{uL}{\alpha}$$

\(Pe>>1\)のときに拡散項を、\(Pe<<1\)のときに移流項を無視できます。

物質ペクレ数 \(Pe_M\)

流れ場の代表速度を\(u\)、代表長さを\(L\)、代表濃度差を\(\Delta C\)とすると、質量流束の移流項と拡散項は以下のようになります。

$$(移流項)=(濃度) \times (流速)=\Delta C u$$

$$(拡散項)=-D \frac{\partial C}{\partial x}=D \frac{\Delta C}{L}=\frac{D \Delta C}{L}$$

従って、質量流束の移流項と拡散項の比で定義される物質ぺクレ数\(Pe_M\)は以下のようになります。

$$Pe_M=\frac{\Delta C u}{\lambda \Delta T / L}=\frac{u L}{D}$$

\(Pe_M>>1\)のときに拡散項を、\(Pe_M<<1\)のときに移流項を無視できます。

レイノルズ数 \(Re\)

円管流れにおいて、平均流速を\(\overline{u}\)、管の内径を\(L\)とすると、運動量流束の移流項と拡散項、すなわち慣性力と粘性力は以下のようになります。

$$(慣性力)=(単位体積あたりの運動量) \times (平均流速)=\rho \overline{u} \times \overline{u}=\rho \overline{u}^2$$

$$(拡散項)=-\mu \frac{\partial u}{\partial r}=\mu \frac{\overline{u}}{L}=\frac{\mu \overline{u}}{L}$$

従って、慣性力と粘性力の比で定義されるレイノルズ数\(Re\)は以下のようになります。

$$Re=\frac{\rho \overline{u}^2}{\mu \overline{u} / L}=\frac{\rho \overline{u} L}{\mu}=\frac{\overline{u} L}{\mu/\rho}=\frac{\overline{u} L}{\nu}$$

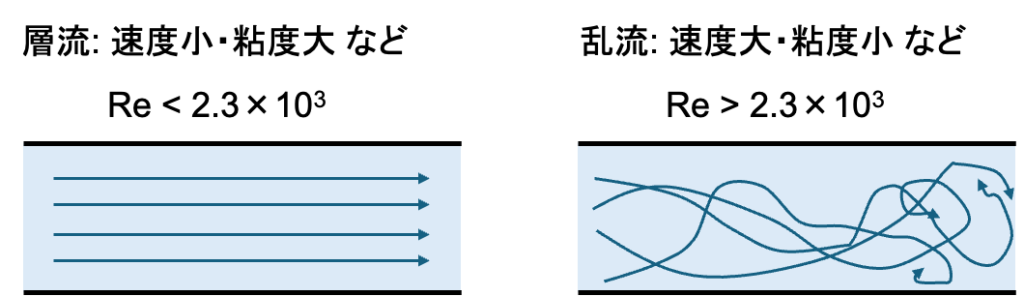
\(Re\)は流れの特徴を表す無次元数であり、\(Re\)が小さいと流体が規則正しく流れる層流、\(Re\)が大きいと流体が不規則に流れる乱流となります。円管の流れが層流から乱流に遷移する\(Re\)は2300〜4000程度であることが知られています（円管流れの問題文では2300より大きいか小さいかで決めていいことが多いです）。

伝達流束と拡散流束の比

物質量伝達とは

壁面に沿って流体の流れがあるとき、壁面と流体間のある物質量の差を推進力とし、物質量の移動が生じます。ただし、固体表面と流体の間の物質量の伝わりやすさは一様ではなく、物性値以外の流れの様子や表面状態によっても変化します。

従って、伝達する物質量流束を表す式は、固体表面と流体の単純な物質量差に比例するとし、さまざまな周囲環境により定まる値を伝達係数としてひとまとめに扱います。

また、伝達流束と拡散流束の比から一連の無次元数が求められます。

ヌッセルト数 \(Nu\)

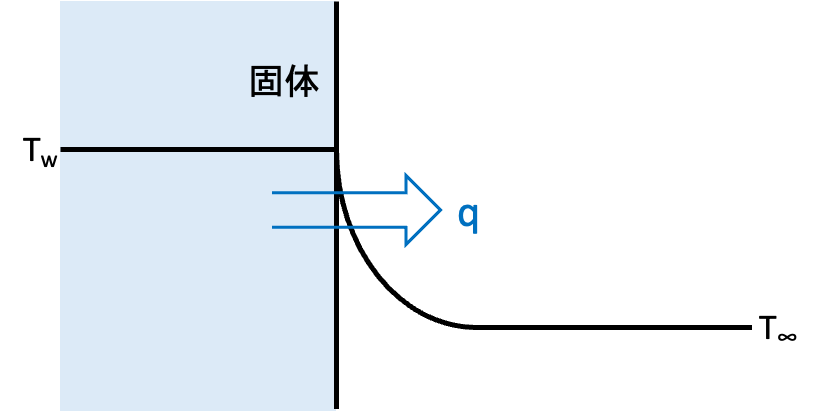
熱伝達による固体から流体への熱流束は以下のようになります。

$$q=h(T_w-T_\infty)$$

このとき、

\(q [J/(m^2 \cdot s])\): 熱流束

\(T_w [K]\): 固体表面の温度

\(T_\infty [K]\): 遠方での流体の温度

\(h [J/(m^2 \cdot s \cdot K)]\): 熱伝達率、熱伝達係数（物性値ではなく実験的に求まる値)

を表しています。

代表長さを\(L\)、代表温度差を\(\Delta T\)とすると、熱伝達と熱伝導のそれぞれの熱流束は以下のようになります。

$$q_{熱伝達} =h \Delta T$$

$$q_{熱伝導} =-\lambda \frac{\partial T}{\partial x}=\lambda \frac{\Delta T}{L}=\frac{\lambda \Delta T}{L}$$

従って、熱伝達流束と熱伝導流束の比で定義されるヌッセルト数\(Nu\)は以下のようになります。

$$Nu=\frac{q_{熱伝達}}{q_{熱伝導}}=\frac{h\Delta T}{\lambda \Delta T/L}=\frac{hL}{\lambda}$$

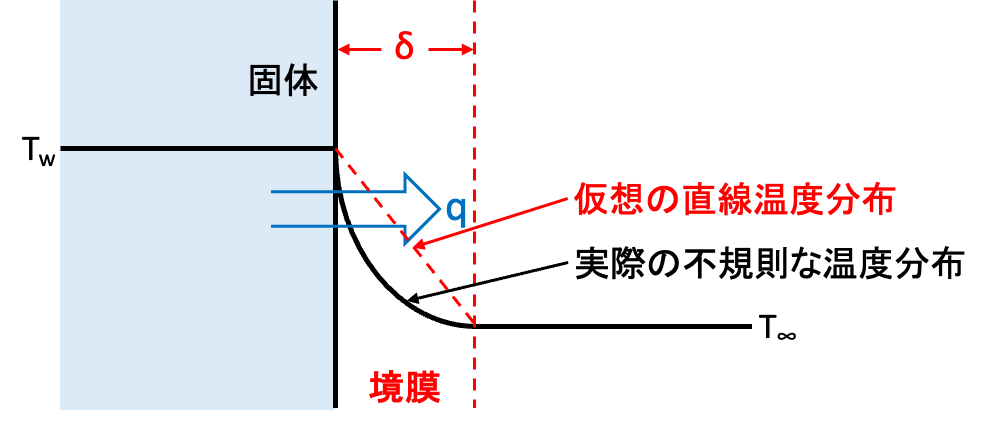
ここで、境膜内に仮想の直線温度分布を考え、仮想の境膜厚みを\(\delta\)とします。境膜内の熱流束にフーリエの法則を用いて、

$$q_{熱伝達}=\lambda \frac{T_w-T_\infty}{\delta}=\frac{\lambda}{\delta}(T_w-T_\infty)$$

熱伝達係数を用いた式と比較することで以下の関係式が得られます。

$$h=\frac{\lambda}{\delta} \Rightarrow \delta=\frac{\lambda}{h}$$

また、\(Nu\)の式を変形すると、

$$Nu=\frac{hL}{\lambda}=\frac{L}{\lambda/h}=\frac{L}{\delta}$$

従って、\(Nu\)は代表長さと境膜厚みの比であると捉えられます。\(Nu\)が大きいほど自然対流による熱伝達の効果が大きい、もしくは境膜厚みが薄いと言えます。

\(Nu\)には経験則から得られた近似式が存在します。例えば、平板と一様な流れに対して以下の式が成り立ちます。¹

$$\begin{equation}Nu= \begin{cases}
0.664Re^\frac{1}{2} Pr^\frac{1}{3} \quad (Re<3.2\times10^5) \\
0.037Re^{0.8} Pr^\frac{1}{3} \quad (Re>3.2\times10^5)
\end{cases}\end{equation}$$

また、球体が一様な流れの中にある場合、以下のランツ・マーシャルの式が成り立ちます。²

$$Nu=2+0.6Re^\frac{1}{2} Pr^\frac{1}{3} \quad (Re<1000)$$

式を見ると分かるように、物性値で求まる\(Re\)や\(Pr\)を用いて、周辺環境で定まる\(Nu\)を求められるのがこれらの近似式の有用性となります。

1. 代表長さと代表速度は平板先端からの距離および一様流の速度 ↩︎
2. 代表長さは球の直径 ↩︎

シャーウッド数 \(Sh\)

物質伝達による固体から流体への物質流束は以下のようになります。

$$J=k_c(C_w-C_\infty)$$

このとき、

\(J [kg/(m^2 \cdot s])\): 物質流束

\(C_w [kg/m^3]\): 固体表面の濃度

\(C_\infty [kg/m^3]\): 遠方での流体の濃度

\(k_c [m/s)]\): 物質伝達率、物質伝達係数（物性値ではなく実験的に求まる値)

を表しています。

代表長さを\(L\)、代表濃度差を\(\Delta C\)とすると、物質伝達と物質拡散のそれぞれの物質流束は以下のようになります。

$$J_{物質伝達} =k_c \Delta C$$

$$J_{物質拡散} =-D \frac{\partial C}{\partial x}=D \frac{\Delta C}{L}=\frac{D \Delta C}{L}$$

従って、物質伝達流束と物質拡散流束の比で定義されるシャーウッド数\(Sh\)は以下のようになります。

$$Sh=\frac{J_{物質伝達}}{J_{物質拡散}}=\frac{k_c\Delta C}{D \Delta C/L}=\frac{k_c L}{D}$$

ここで、境膜内に仮想の直線温度分布を考え、仮想の境膜厚みを\(\delta\)とします。境膜内の物質流束にフィックの第一法則を用いて、

$$J_{熱伝達}=D \frac{C_w-C_\infty}{\delta}=\frac{D}{\delta}(C_w-C_\infty)$$

物質伝達係数を用いた式と比較することで以下の関係式が得られます。

$$k_c=\frac{D}{\delta} \Rightarrow \delta=\frac{D}{k_c}$$

また、\(Sh\)の式を変形すると、

$$Sh=\frac{k_c L}{D}=\frac{L}{D/k_c}=\frac{L}{\delta}$$

従って、\(Sh\)は代表長さと境膜厚みの比であると捉えられます。\(Sh\)が大きいほど自然対流による物質伝達の効果が大きい、もしくは境膜厚みが薄いと言えます。

\(Sh\)には経験則から得られた近似式が存在します。例えば、平板と一様な流れに対して以下の式が成り立ちます。

$$\begin{equation}Sh=\begin{cases}
0.664Re^\frac{1}{2} Sc^\frac{1}{3} \quad (Re<3.2\times10^5) \\
0.037Re^{0.8} Sc^\frac{1}{3} \quad (Re>3.2\times10^5)
\end{cases}\end{equation}$$

また、球体が一様な流れの中にある場合、以下のランツ・マーシャルの式が成り立ちます。

$$Sh=2+0.6Re^\frac{1}{2} Sc^\frac{1}{3} \quad (Re<1000)$$

式を見ると分かるように、物性値で求まる\(Re\)や\(Sc\)を用いて、周辺環境で定まる\(Sh\)を求められるのがこれらの近似式の有用性となります。

まとめ

今回は基本の無次元数について紹介しました。他にも無次元数はまだまだありますが、まずはこれらの無次元数をしっかり押さえましょう。